Entropia

Entropia jest miarą nieuporządkowania lub niepewności w rozkładzie prawdopodobieństwa. Pojęcie to zostało po raz pierwszy przedstawione w 1854 roku przez fizyka Rudolfa Clausiusa, zajmującego się zagadnieniami termodynamiki i w tym znaczeniu definicja entropii odnosi się (w dużym skrócie) do przebiegu procesów spontanicznych. Obecnie pojęcie entropii ma również swoje zastosowanie w statystyce. Pozwala nam ona bowiem określić swego rodzaju różnorodność w zbiorze danych.

Entropia w statystyce

Analizując zmienne jakościowe, miara entropii daje nam informację na temat tego, jak wiele zmienności (a więc „nieporządku”) wprowadzają poszczególne zmienne. Otrzymujemy wskaźnik stopnia losowości poszczególnych zmiennych jakościowych. Entropia została wprowadzona do dziedziny statystyki na gruncie teorii informacji, a jedną z najczęściej wykorzystywanych jej miar jest entropia Shannona.

Jeśli wynik entropii wynosi 0, oznacza to, że zmienna przyjmuje tylko jedną wartość. Takie zmienne nazywamy stałymi – nie pozwalają one na otrzymanie żadnych dodatkowych informacji.

Im wskaźnik entropii jest wyższy, tym większa różnorodność kategorii, które przyjmuje zmienna. Wynik będzie zależał od ilości unikalnych kategorii analizowanej zmiennej oraz częstości ich występowania w odniesieniu do wszystkich obserwacji. Wartość entropii nie jest zależna natomiast od wielkości zbioru – jeśli zmienna posiada cztery kategorie, stanowiące odpowiednio 40%, 30%, 20% oraz 10% rozkładu, to entropia będzie miała taką samą wartość, niezależnie czy obserwacji mamy 10 czy 10 000.

Procentowa wartość entropii

Otrzymany wynik entropii można przedstawić również w formie procentowej, w porównaniu do jej wartości maksymalnej. Osiągnięcie największej możliwej wartości (100% maksymalnej wartości entropii) informuje nas o tym, że wszystkie wartości zmiennej są równie prawdopodobne. Takim przypadkiem jest sytuacja, gdy w danym zbiorze każda obserwacja posiada inny wynik (kategorię) analizowanej zmiennej lub wszystkie jej kategorie są w inny sposób równoliczne.

Jako, że wartość entropii sama w sobie nie jest łatwo interpretowalna, warto przedstawić ten wynik w postaci procentowej – wiemy wówczas, że maksymalna wartość to 100% i jest to nasz punkt odniesienia do intepretowania otrzymanego wyniku.

Tabela 1. Wyniki entropii dla analizowanej zmiennej

Spójrzmy na przykład przedstawiony w Tabeli 1. – entropia dla analizowanej zmiennej stopnia ukończonych studiów wynosi 1,28. Wynik ten nie jest bliski 0, a więc z pewnością w rozkładzie znajduje się pewny nieporządek czy też niepewność.

Jeśli jednak nie znamy wyników entropii dla innych zmiennych, aby np. wybrać do analizy te, które będą wprowadzać najwięcej zmienności, sama wartość 1,28 niewiele więcej nam powie.

Wiedząc, że wynik ten w porównaniu z wartością maksymalną stanowi 92,3% otrzymujemy dodatkowo informację, że znacząco zróżnicowane są zarówno wartości zmiennej, jak i liczebności poszczególnych kategorii.

Jak otrzymać wartość entropii

Jeśli znamy miary entropii dla poszczególnych zmiennych jakościowych, możemy ich użyć jako np. wskaźnika ważności zmiennych. Taką informację można wykorzystać np. w modelowaniu czy klasyfikacji. Wartość entropii możemy uzyskać m. in. w procedurze Audyt danych w PS IMAGO PRO. Wszystkie analizowane zmienne jakościowe są podsumowane w jednej tabeli, co umożliwia szybkie porównanie otrzymanych wyników i wybranie do swojego modelu najbardziej obiecujących zmiennych.

W jaki jednak dokładnie sposób wyliczana jest entropia? Jak już powiedzieliśmy, kluczowa jest tu ilość unikalnych kategorii zmiennej oraz ich udział w jej rozkładzie. Wzór na entropię Shannona, czyli najczęściej wykorzystywany wzór na entropię zmiennej jakościowej, jest następujący:

gdzie H(X) oznacza entropię zmiennej X, a p(x) oznacza prawdopodobieństwo wystąpienia wartości x.

Entropia, którą otrzymujemy w procedurze Audyt danych w PS IMAGO PRO (tab. 1) wyliczana jest na podstawie logarytmu naturalnego. Jej wzór wygląda zatem następująco:

gdzie H(X) oznacza entropię zmiennej X, a p(x) oznacza prawdopodobieństwo wystąpienia wartości x.

Aby wzór ten był bardziej zrozumiały, przedstawmy go na przykładzie. Chcemy wyliczyć entropię dla zmiennej jakościowej jaką jest stopień ukończonych studiów (X = studia). Nasz zbiór składa się z 10 obserwacji: 4 licencjatów, 3 inżynierów, 2 magistrów oraz 1 doktora (rys. 1). Prawdopodobieństwo przynależności do kategorii licencjat wynosi 40%, a więc pierwsza część równania będzie wynosiła . Dodając analogicznie kolejne elementy wzoru dla poszczególnych kategorii otrzymamy następujące równanie:

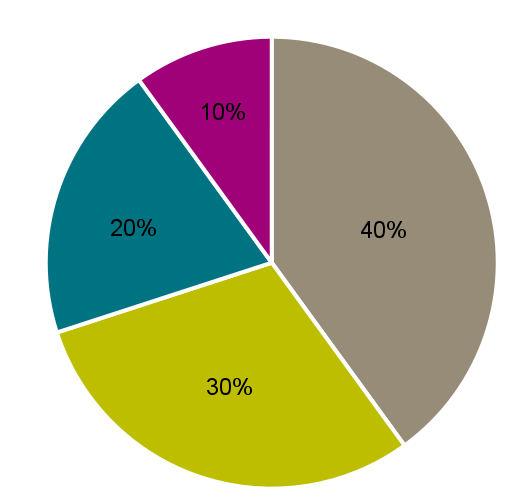
Rysunek 1. Rozkład kategorii zmiennej

Maksymalna wartość entropii wynosi ln(n), gdzie n to liczba kategorii danej zmiennej jakościowej. W naszym przypadku zmienna jakościowa ma 4 kategorie, a więc największa wartość entropii możliwa do uzyskania wynosi ln(4) = 1,39.
Gdybyśmy chcieli przedstawić wynik entropii w porównaniu z wartością maksymalną, to wynosić on będzie w zaokrągleniu  (tab. 1).

Podsumowanie

Entropia jest miarą niepewności lub nieporządku w rozkładzie prawdopodobieństwa. Jedną z jej najczęściej wykorzystywanych miar jest entropia Shannona. Maksymalna wartość entropii osiągana jest, gdy rozkład jest równomierny, natomiast minimalna wynosząca 0, gdy rozkład jest deterministyczny.

Należy jednak mieć na względzie, że podstawa logarytmu, w oparciu o który wyliczana jest entropia, może przyjmować różne wartości – np. 2, jak w przypadku wzoru Shannona, 10, czy też ℯ (liczba Eulera, liczba Nepera), gdy wykorzystywany jest logarytm naturalny. Jeśli chcemy porównywać wyniki dla kilku zmiennych, trzeba mieć pewność, że podstawa wykorzystanego we wzorze logarytmu jest taka sama. Alternatywnie, można porównywać ze sobą wyniki entropii w porównaniu z wartością maksymalną – takie wartości wyrażone w procentach zdecydowanie łatwiej jest do siebie odnieść.